Теория вероятности примеры решения задач

Тема 2

ТЕМА 2

ЗАДАЧА № 1

Вычислить вероятность того, что некоторое событие не произойдет, если известно, что при n испытаниях оно в среднем происходит в m случаях.

РЕШЕНИЕ

1) Обозначим событие А = «Событие произошло». Определим вероятность появления данного события. Для этого воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,
n – общее число элементарных несовместных равновозможных исходов.

2) Определим вероятность того, что событие А не произойдет, по формуле:

ОТВЕТ: Вероятность того, что событие не произойдет, равна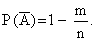

ЗАДАЧА №2

Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов?

РЕШЕНИЕ

1) Обозначим событие А = «Вытянутый студентом билет состоит из подготовленных им билетов». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,
n – общее число элементарных несовместных равновозможных исходов.
2) Определим n. Общее число билетов определяется сочетанием по 2 из 60:

3) Количество билетов, вопросы которых студент знает, определяется сочетанием по 2 из 50:

4) Определим вероятность события А:

ОТВЕТ: Вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов равна Р(А) = 0,69. То есть, если будет, например, 100 таких студентов, то 69 из них вытянут билеты, к вопросам которых они подготовлены.

ЗАДАЧА № 3

Какова вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти?

РЕШЕНИЕ

1) Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,
n – общее число элементарных несовместных равновозможных исходов.

2) Определим n. Для этого воспользуемся формулой сочетания по 4 из 52(так как нас не интересует порядок вытянутых карт):

3) Обозначим событие А = «Из 4 вынутых карт 2 принадлежат пиковой масти». Найдем вероятность вытягивания 2 пиковых карт по формуле сочетания по 2 из 13 (так как всего карт пиковой масти 13):

4) Найдем вероятность вытягивания оставшихся двух карт не пиковой масти по формуле сочетания по 2 из 39 (52-13).

5) Полученные значения мы перемножаем: m = m1 ? m2

m = 78 ? 741 = 57798

6) Найдем вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти:

ОТВЕТ: Вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти, равна 0,21.

Страница 1

Тема 2

Тема 3

Тема 4

Тема 5

Тема 6

Тема 7

Тема 8

Приложение 1

Приложение 2