Тождественные преобразования

Свойства степеней

Для любых x, y и положительных a и b верны равенства: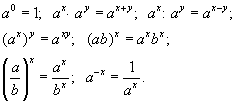

Свойства арифметических корней

Для любых натуральных n и k, больших 1, и любых неотрицательных a и b верны равенства: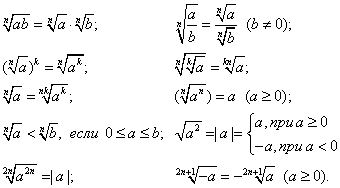

Многочлены

Для любых a, b и c верны равенства: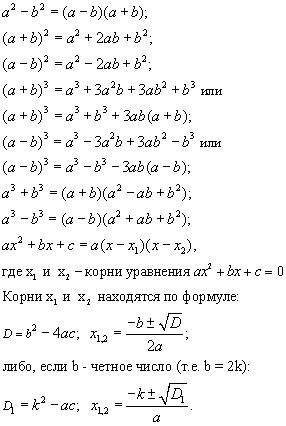

Соотношения между тригонометрическими функциями одного и того же аргумента

(здесь и в дальнейшем запись n є Z означает, что n – любое целое число)

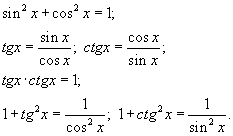Формулы сложения: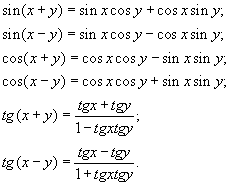

Формулы двойного аргумента: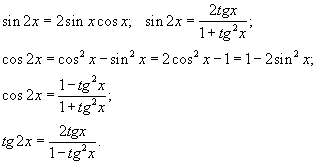

Формулы тройного аргумента: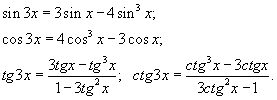

Формулы половинного аргумента:

(для функций sin и cos – формулы понижения степени)

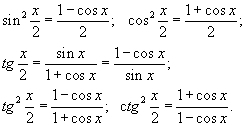Формулы кубов:

Формулы 4-й степени: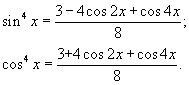

Формулы преобразования суммы в произведение: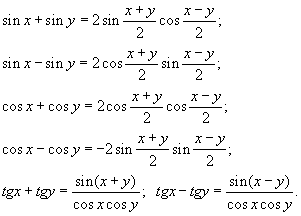

Формулы преобразования произведения в сумму: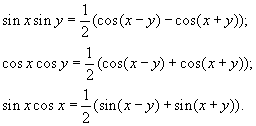

Формула приведения для преобразования выражений вида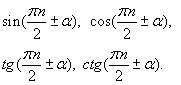

а) перед приведенной функцией ставиться тот знак, который имеет исходная функция;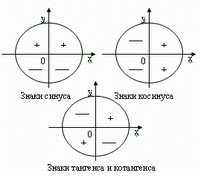

б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.)
Например:

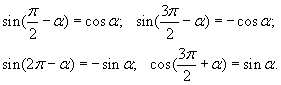Формулы нахождения угла: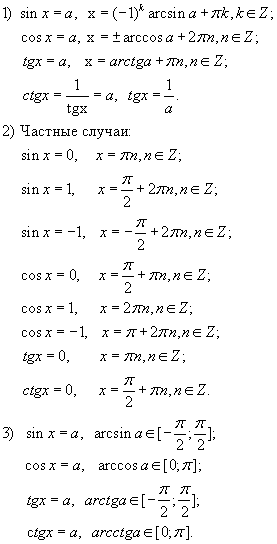