1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле: 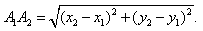 2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам: 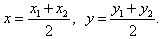 3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид: y = kx + q. Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.
| 4. Общее уравнение прямой имеет вид: ax + by + c = 0. 5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид: ax + by + c = 0. 6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2
соответственно имеют вид:
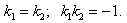 7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид: 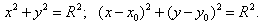 8. Уравнение: 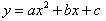 представляет собой уравнение параболы с вершиной в точке, абсцисса которой 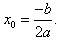 |
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле: 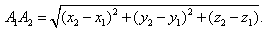 2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам: 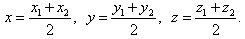 3. Модуль вектора 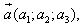 заданного своими координатами, находится по формуле: заданного своими координатами, находится по формуле: 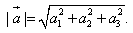 4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы: 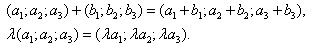 5. Единичный вектор 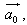 сонаправленный с вектором сонаправленный с вектором 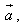 находится по формуле: находится по формуле: 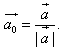 6. Скалярным произведением 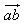 векторов векторов 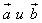 называется число: называется число: 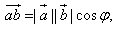 где 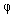 - угол между векторами. - угол между векторами. | 7. Скалярное произведение векторов 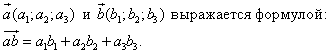 8. Косинус угла между векторами 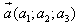 и и 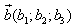 находится по формуле: находится по формуле: 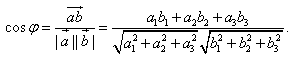 9. Необходимое и достаточное условие перпендикулярности векторов 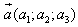 и и 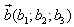 имеет вид: имеет вид: 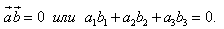 10. Общее уравнение плоскости, перпендикулярной вектору 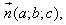 имеет вид: имеет вид: ax + by + cz + d = 0. 11. Уравнение плоскости, перпендикулярной вектору 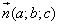 и проходящей через точку (xo;yo;zo), имеет вид: и проходящей через точку (xo;yo;zo), имеет вид: a(x - xo) + b(y - yo) + c(z - zo) = 0. 12. Уравнение сферы с центром O(0;0;0) записывается в виде: 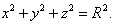
|